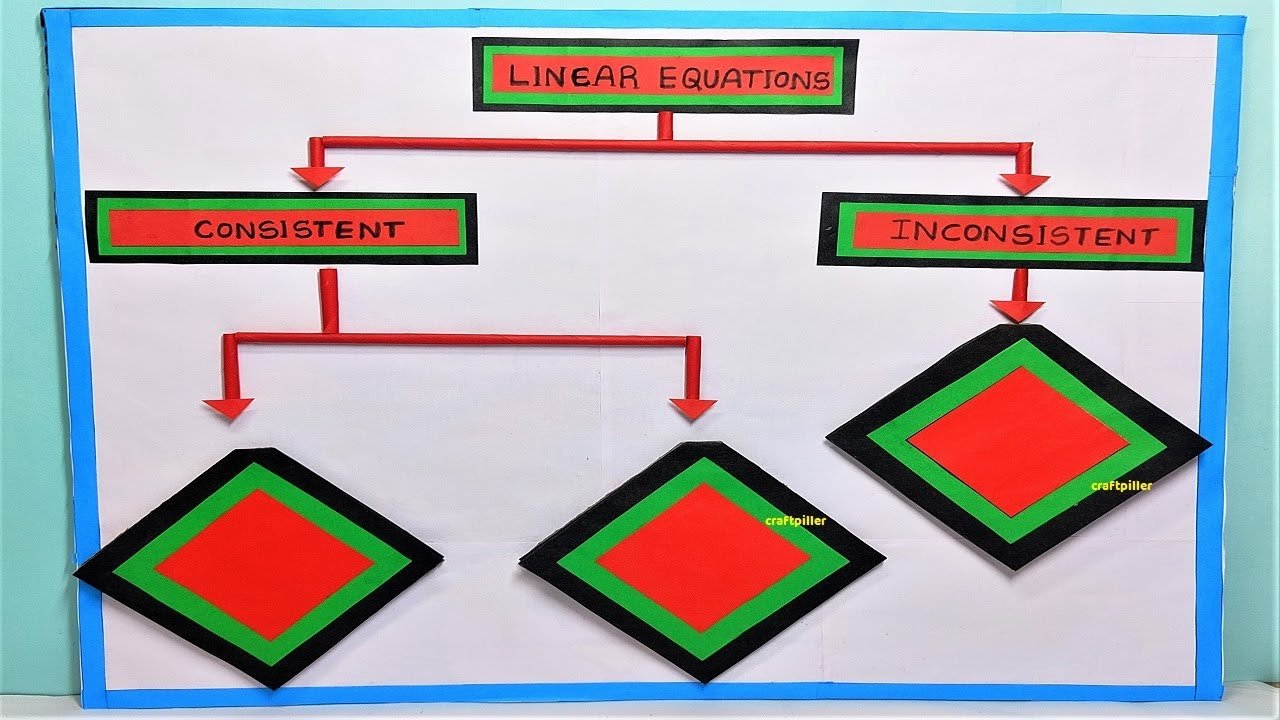
Linear equations are algebraic equations that represent straight lines on a graph. They are called “linear” because their highest power of the variable(s) involved is
1. The general form of a linear equation in one variable (x) is:
ax + b = 0
where ‘a’ and ‘b’ are constants, and ‘x’ is the variable. The solution to a linear equation in one variable is a single value of ‘x’ that makes the equation true.
Examples of linear equations in one variable:
- 2x – 3 = 0
- 4x + 7 = 15
- -3x + 2 = -8
When graphed on the coordinate plane, a linear equation in one variable forms a straight line.
Linear equations can also involve more than one variable and are called “linear equations in two variables” or “simultaneous linear equations.” The general form of a linear equation in two variables (x and y) is:
ax + by = c
where ‘a,’ ‘b,’ and ‘c’ are constants, and ‘x’ and ‘y’ are the variables. The solution to a system of two linear equations is the values of ‘x’ and ‘y’ that satisfy both equations simultaneously, making them true.
Examples of linear equations in two variables:
- 2x + 3y = 10
- 4x – 5y = 8
- -3x + 2y = -6