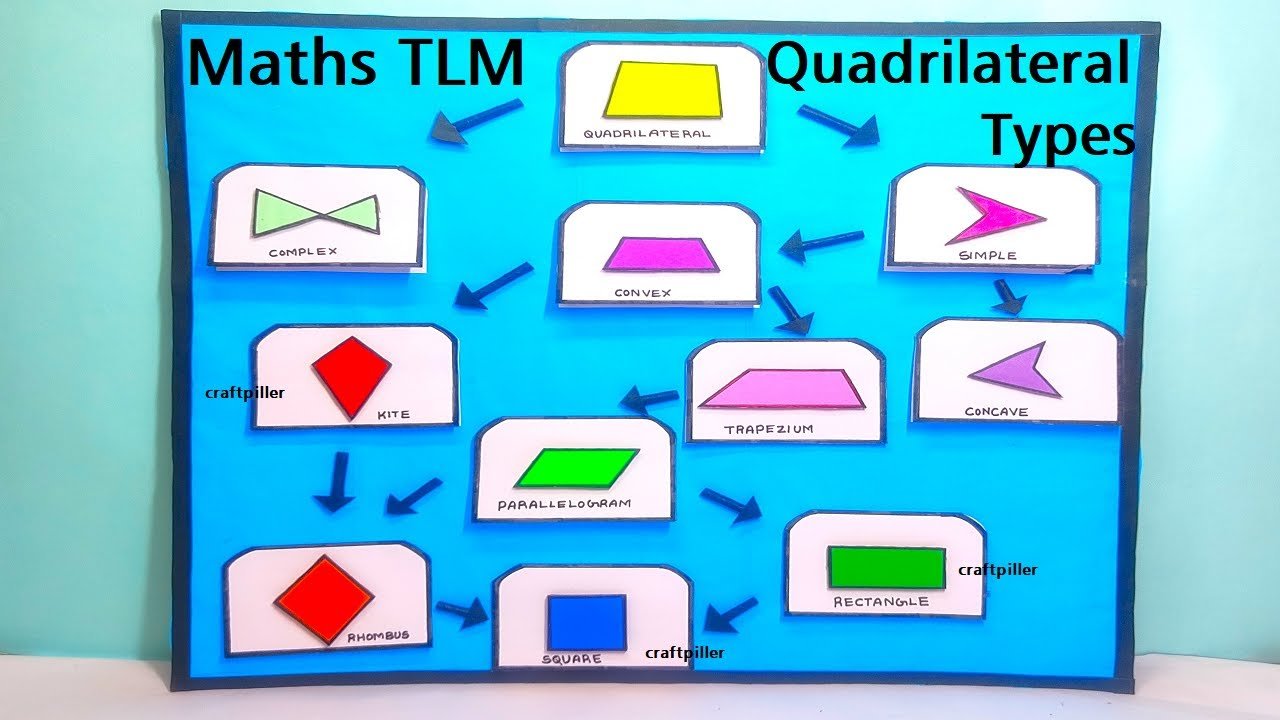
Quadrilaterals are four-sided polygons, and there are several types of quadrilaterals, each with its unique characteristics and properties.
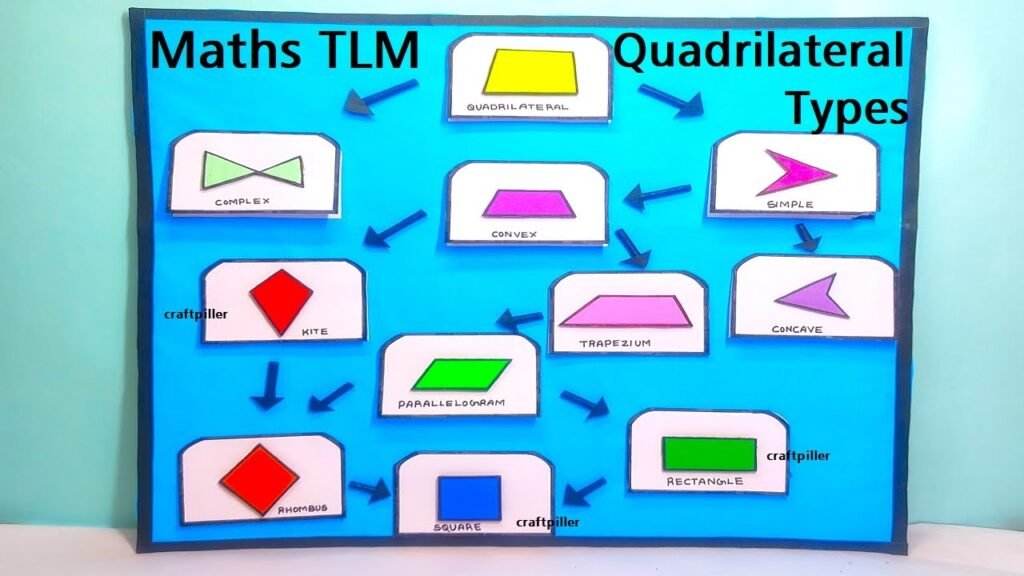
Here are some common types of quadrilaterals:
- Rectangle: A rectangle is a quadrilateral with four right angles (90-degree angles). Opposite sides of a rectangle are equal in length, and all angles are congruent. The diagonals of a rectangle are also equal in length and bisect each other.
- Square: A square is a special type of rectangle with all sides of equal length. Therefore, all angles in a square are right angles (90 degrees). The diagonals of a square are congruent and bisect each other at right angles.
- Parallelogram: A parallelogram is a quadrilateral with opposite sides that are parallel to each other. Opposite angles are also equal in measure. Parallelograms do not have any specific requirements for angle sizes or side lengths.
- Rhombus: A rhombus is a parallelogram with all sides of equal length. Therefore, it is also a type of equilateral quadrilateral. The diagonals of a rhombus bisect each other at right angles.
- Trapezoid: A trapezoid is a quadrilateral with one pair of parallel sides. The other two sides are not parallel. Trapezoids do not have any specific requirements for angle sizes or side lengths.
- Isosceles Trapezoid: An isosceles trapezoid is a trapezoid with two sides of equal length. The base angles (the angles adjacent to the non-parallel sides) are also congruent.
- Kite: A kite is a quadrilateral with two pairs of equal-length adjacent sides. The diagonals of a kite intersect at a right angle, and one diagonal bisects the other.
- Rectangle (Oblique): A rectangle with no right angles is known as an oblique rectangle. It still has opposite sides of equal length and congruent diagonals.
- Square (Oblique): A square with no right angles is called an oblique square. It still has all sides of equal length and congruent diagonals.
Each type of quadrilateral has specific properties and relationships between its sides and angles. Understanding these properties is essential for solving geometric problems and working with shapes in various applications, such as architecture, engineering, and design.
Step by step video making on quadrilateral types working model – maths tlm for exhibition
#quadrilateral #types #workingmodel #mathstlm #exhibition #diy #craftpiller #maths #tlm