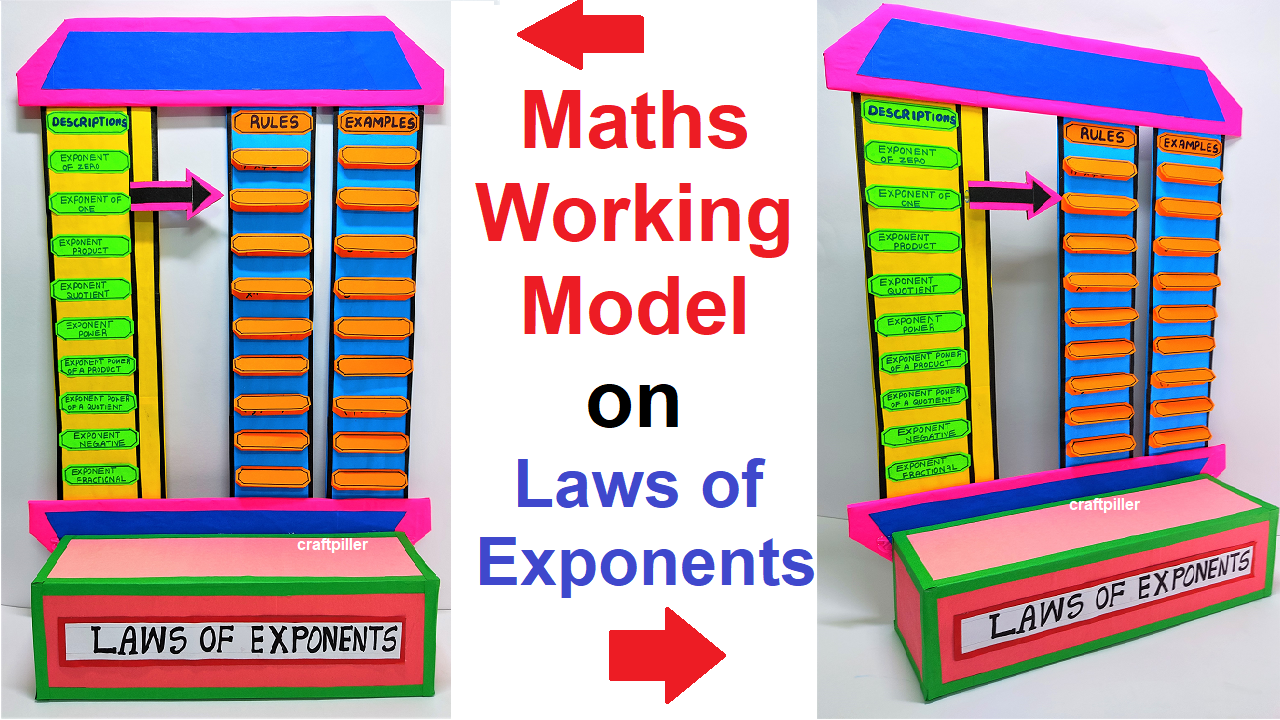
The laws of exponents, also known as the rules of exponents or exponentiation rules, are fundamental rules that govern the manipulation of exponential expressions.
These laws make it easier to simplify and perform various operations with expressions involving exponents.
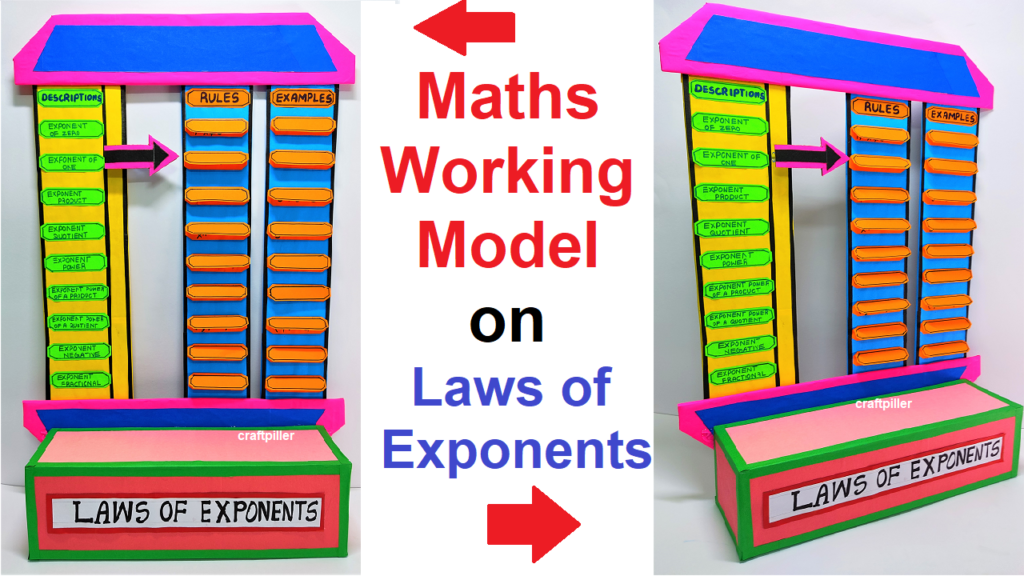
The laws of exponents apply to expressions of the form “a^n,” where “a” is the base and “n” is the exponent (a positive or negative whole number, or zero).
Below are the main laws of exponents:
- Product Law: When multiplying two exponential expressions with the same base, add the exponents. a^m * a^n = a^(m + n)Example: 2^3 * 2^4 = 2^(3 + 4) = 2^7 = 128
- Quotient Law: When dividing two exponential expressions with the same base, subtract the exponents. a^m / a^n = a^(m – n)Example: 5^6 / 5^2 = 5^(6 – 2) = 5^4 = 625
- Power to a Power Law: When raising an exponential expression to another exponent, multiply the exponents. (a^m)^n = a^(m * n)Example: (3^2)^3 = 3^(2 * 3) = 3^6 = 729
- Zero Exponent Law: Any nonzero base raised to the power of zero is equal to 1. a^0 = 1 (where “a” ≠ 0)Example: 7^0 = 1
- Negative Exponent Law: To get the reciprocal of an exponential expression, change the sign of the exponent. a^(-n) = 1 / a^n (where “a” ≠ 0)Example: 2^(-3) = 1 / 2^3 = 1 / 8 = 0.125
- Multiplication by Zero: Any nonzero base raised to a negative exponent will result in a fraction with 1 as the numerator and the base raised to the positive exponent as the denominator. a^(-n) = 1 / (a^n) (where “a” ≠ 0)Example: 4^(-2) = 1 / 4^2 = 1 / 16
These laws are essential for simplifying expressions involving exponents, solving equations, and understanding the properties of exponential functions.
They form the basis for many mathematical concepts and applications in various fields, including algebra, calculus, and sciences.
#mathsworkingmodel #mathstlm #lawsofexponent #lawsofexponents #craftpiller #diy