how to make maths tlm working model project (real number system ) – diy – simple easy | craftpiller

Creating a tangible learning model (TLM) for the real number system using cardboard and color paper can be a fun and effective way to understand this mathematical concept.

Here’s a step-by-step guide to making the TLM:

Materials Needed:

1. Cardboard sheet
2. Color papers (representing different categories of numbers)
3. Scissors
4. Glue
5. Marker
6. Ruler

Procedure:

Step 1: Prepare the Base

• Take a piece of cardboard and cut it into a rectangular base. This will serve as the foundation for your TLM.

Step 2: Define Categories of Numbers

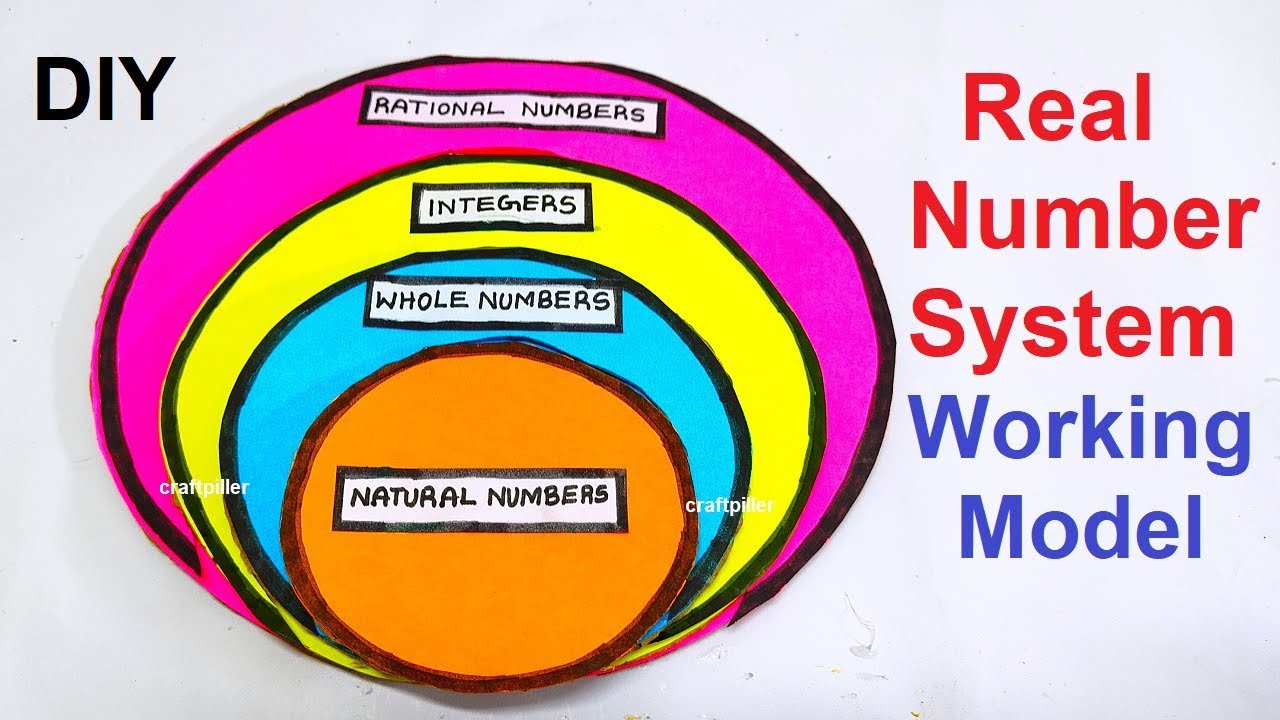
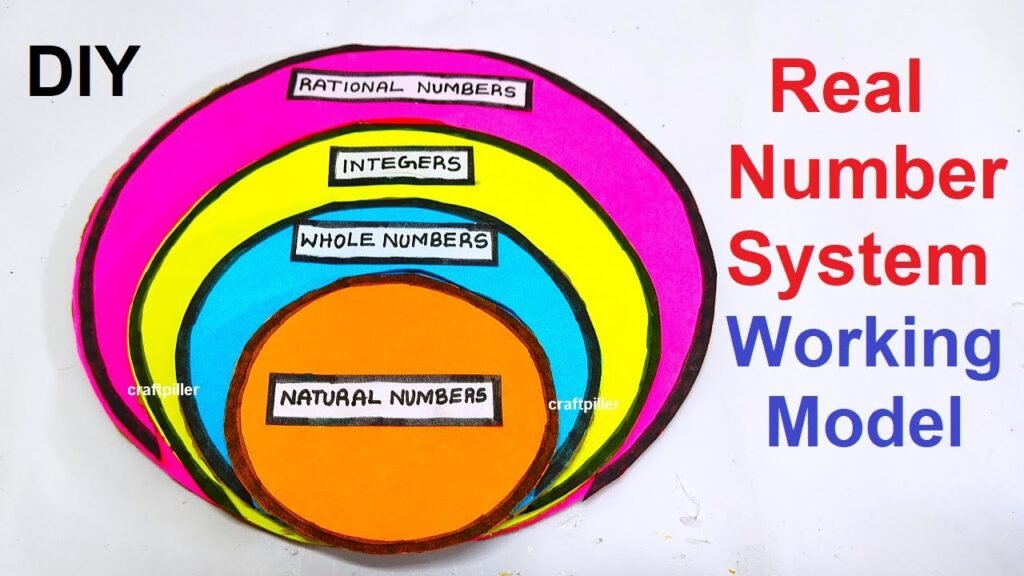
• Use different color papers to represent various categories of numbers:
  • Orange paper: Representing natural numbers
  • Blue paper: Representing whole numbers
  • Yellow paper: Representing integers
  • Pink paper: Representing rational numbers

Step 3: Create Number Tiles

• Cut the colored papers into square tiles, making sure each color represents its respective category of numbers. Write down examples of numbers from each category on the corresponding colored tiles.
  • For example:
    • Orange Tiles (Natural Numbers):
      • Tile 1: “1”
      • Tile 2: “2”
      • Tile 3: “3”
      • …
    • Blue Tiles (Whole Numbers):
      • Tile 1: “0”
      • Tile 2: “1”
      • Tile 3: “2”
      • …
    • Yellow Tiles (Integers):
      • Tile 1: “-3”
      • Tile 2: “-2”
      • Tile 3: “-1”
      • …
    • Pink Tiles (Rational Numbers):
      • Tile 1: “1/2”
      • Tile 2: “0.75”
      • Tile 3: “-3/4”
      • ..

Step 4: Arrange Tiles

• Place the tiles on the cardboard base in an organized manner, forming a visual representation of the real number system.

Definition and Examples:

• Real Numbers (R): The set of all rational and irrational numbers. This includes numbers like fractions, decimals, square roots, and more.
  • Examples: √2, -3/4, 0.5, π, -√3, etc.
• Rational Numbers (Q): Numbers that can be expressed as the quotient or fraction of two integers.
  • Examples: 1/2, -3/5, 0.75, 2, -7, etc.
• Irrational Numbers (I): Numbers that cannot be expressed as a fraction of two integers. They have non-repeating, non-terminating decimal expansions.
  • Examples: √2, π, e, etc.
• Integers (Z): The set of positive whole numbers, negative whole numbers, and zero.
  • Examples: -3, -2, -1, 0, 1, 2, 3, etc.
• Whole Numbers (W): The set of positive whole numbers and zero.
  • Examples: 0, 1, 2, 3, 4, 5, etc.
• Natural Numbers (N): The set of positive counting numbers.
  • Examples: 1, 2, 3, 4, 5, 6, etc.

By creating this real number systems math’s working model or TLM,

students can visually see the relationships between different categories of numbers and gain a better understanding of the real number system.

https://www.youtube.com/@craftpiller