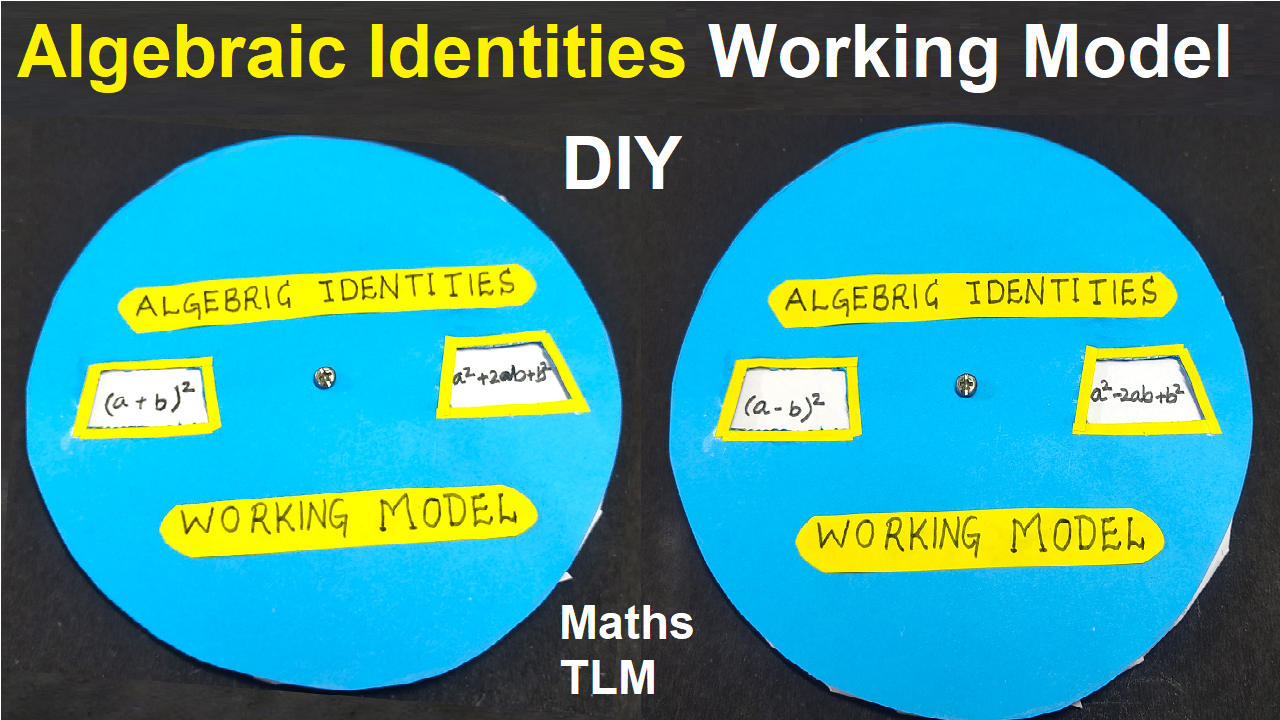
how to make algebraic identities working model – math’s project – tlm – diy | DIY pandit

by

Creating a working model to demonstrate algebraic identities using cardboard and two holes can be an interesting and visual way to showcase mathematical concepts.

Here’s a simple DIY project for an algebraic identities working model:

Materials Needed:

  1. Cardboard
  2. Ruler
  3. Pencil
  4. Scissors
  5. String or yarn
  6. Markers
  7. Colored paper
  8. Glue or tape
  9. Compass
  10. Brass fasteners (optional)

Steps to Create the Algebraic Identities Working Model:

Step 1: Cut Cardboard:

  • Cut a large piece of cardboard to serve as the base for your working model.

Step 2: Draw Circles:

  • Use a compass to draw two circles on the cardboard. These will represent the holes.

Step 3: Cut Holes:

  • Cut out the circles to create the holes in the cardboard.

Step 4: Label the Circles:

  • Label each hole with a variable, such as ‘a’ and ‘b,’ to represent the algebraic expressions.

Step 5: Create Flaps:

  • Cut rectangular flaps on the cardboard around each hole, leaving enough space to write or attach the algebraic expressions.

Step 6: Write or Attach Expressions:

  • Write the algebraic expressions corresponding to each identity on the flaps or attach colored paper with the expressions.

Step 7: Attach Strings:

  • Cut two pieces of string or yarn, and thread them through the holes. Tie knots on the backside to secure them.

Step 8: Display and Explain:

  • Set up your working model at the exhibition table.
  • Pull the strings through the holes to visually demonstrate the algebraic identities.

Step 9: Optional – Brass Fasteners:

  • Instead of string, you can use brass fasteners to attach the expressions to the holes, allowing for easy rotation.

Explanation:

  • During your exhibition, explain each algebraic identity and how pulling the strings or rotating the expressions visually demonstrates the validity of the identities.

This working model provides a tangible representation of algebraic identities, making it an engaging and interactive display for a math project or exhibition. It allows students and visitors to physically manipulate the expressions, enhancing their understanding of algebraic concepts.

https://www.youtube.com/@diypandit

Leave a Comment