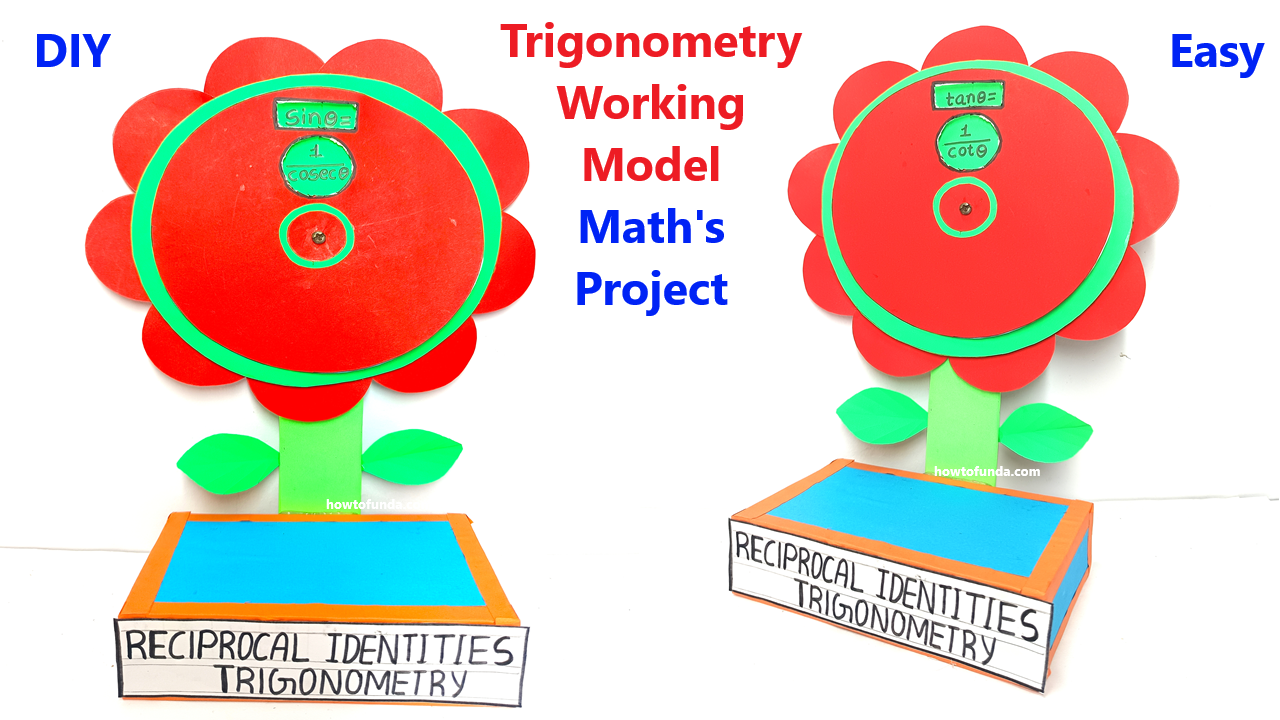
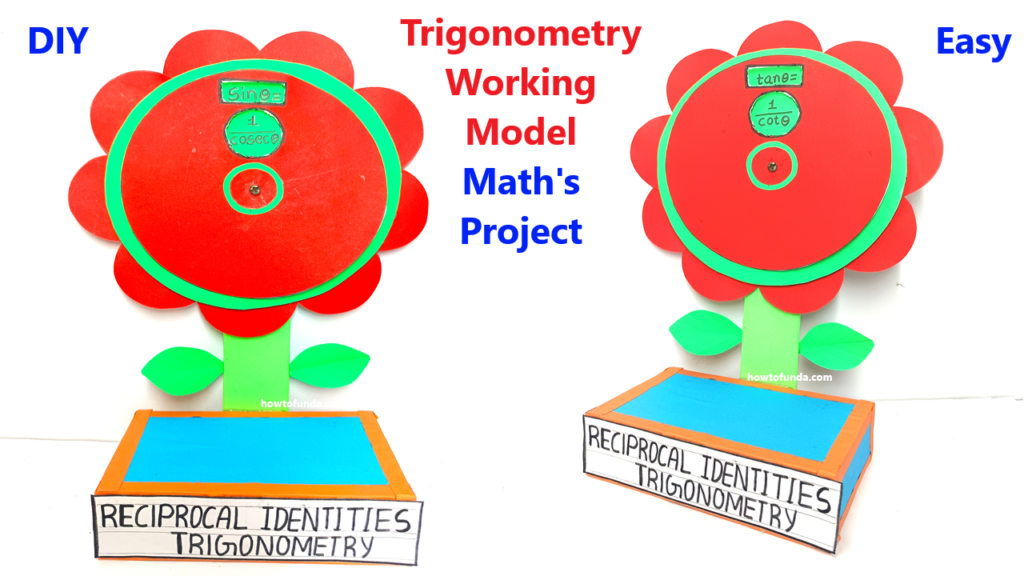
how to make Trigonometric Identities Working Model

by

Here’s a Trigonometric Identities Working Model design idea in a rotating flower format, using color paper, a push pin, and cardboard. This model will visually represent trigonometric identities, making it interactive and engaging.

Concept:

The model displays major trigonometric identities in a flower-like structure, where each petal represents one identity. The petals are attached to a rotating center so students can turn it to view different identities.

Materials Needed:

  1. Cardboard: For the base and flower structure.
  2. Colored Paper: For the petals and decoration.
  3. Push Pin: To create the rotating mechanism.
  4. Marker/Pens: For writing the identities and labeling.
  5. Glue or Tape: To fix materials in place.
  6. Protractor Template: To help with circular symmetry.

Design Overview:

  • A large circular flower with colored petals that rotate around a central hub.
  • Each petal displays a trigonometric identity, such as:
    • sin⁡2θ+cos⁡2θ=1\sin^2\theta + \cos^2\theta = 1sin2θ+cos2θ=1
    • 1+tan⁡2θ=sec⁡2θ1 + \tan^2\theta = \sec^2\theta1+tan2θ=sec2θ
    • 1+cot⁡2θ=csc⁡2θ1 + \cot^2\theta = \csc^2\theta1+cot2θ=csc2θ
  • The rotating mechanism allows users to turn the petals and explore each identity.

Step-by-Step Instructions:

1. Prepare the Base:

  • Cut a circular base out of cardboard (approx. 10–12 inches in diameter).
  • Cover the base with color paper for a clean look.
  • Divide the circle into equal sections using a protractor, one for each petal (e.g., 6 sections for 6 petals).

2. Create the Flower Petals:

  • Cut petal shapes from colored paper (each about 4–5 inches long).
  • Write one trigonometric identity on each petal, such as:
    1. sin⁡2θ+cos⁡2θ=1\sin^2\theta + \cos^2\theta = 1sin2θ+cos2θ=1
    2. 1+tan⁡2θ=sec⁡2θ1 + \tan^2\theta = \sec^2\theta1+tan2θ=sec2θ
    3. 1+cot⁡2θ=csc⁡2θ1 + \cot^2\theta = \csc^2\theta1+cot2θ=csc2θ
    4. sin⁡(90∘−θ)=cos⁡θ\sin(90^\circ – \theta) = \cos\thetasin(90∘−θ)=cosθ
    5. tan⁡θ=sin⁡θcos⁡θ\tan\theta = \frac{\sin\theta}{\cos\theta}tanθ=cosθsinθ​
    6. cot⁡θ=cos⁡θsin⁡θ\cot\theta = \frac{\cos\theta}{\sin\theta}cotθ=sinθcosθ​
  • Decorate the petals with borders or designs to make them visually appealing.

3. Assemble the Rotating Mechanism:

  • Cut a small circle (about 2 inches in diameter) from cardboard for the center hub.
  • Attach the petals around the edge of this circle using glue or tape, ensuring they can fan out evenly.
  • Place the hub in the center of the base and fix it with a push pin. The pin should allow the hub (and attached petals) to rotate freely.

4. Label the Base:

  • Write the title “Trigonometric Identities” at the top of the base.
  • Below the rotating flower, add a short description like:
    “Explore the fundamental relationships of trigonometry by rotating the petals!”

5. Add Interactive Arrows:

  • Use small paper arrows or markers to indicate the rotation direction on the base. This helps guide users on how to interact with the model.

Demonstration:

  1. Rotate the flower petals to display one identity at a time.
  2. Explain the mathematical relationship and real-life applications of each identity (e.g., in physics, engineering, or geometry).
  3. Highlight how the identities connect to form the foundation of trigonometry.

https://www.youtube.com/@howtofunda

Leave a Comment