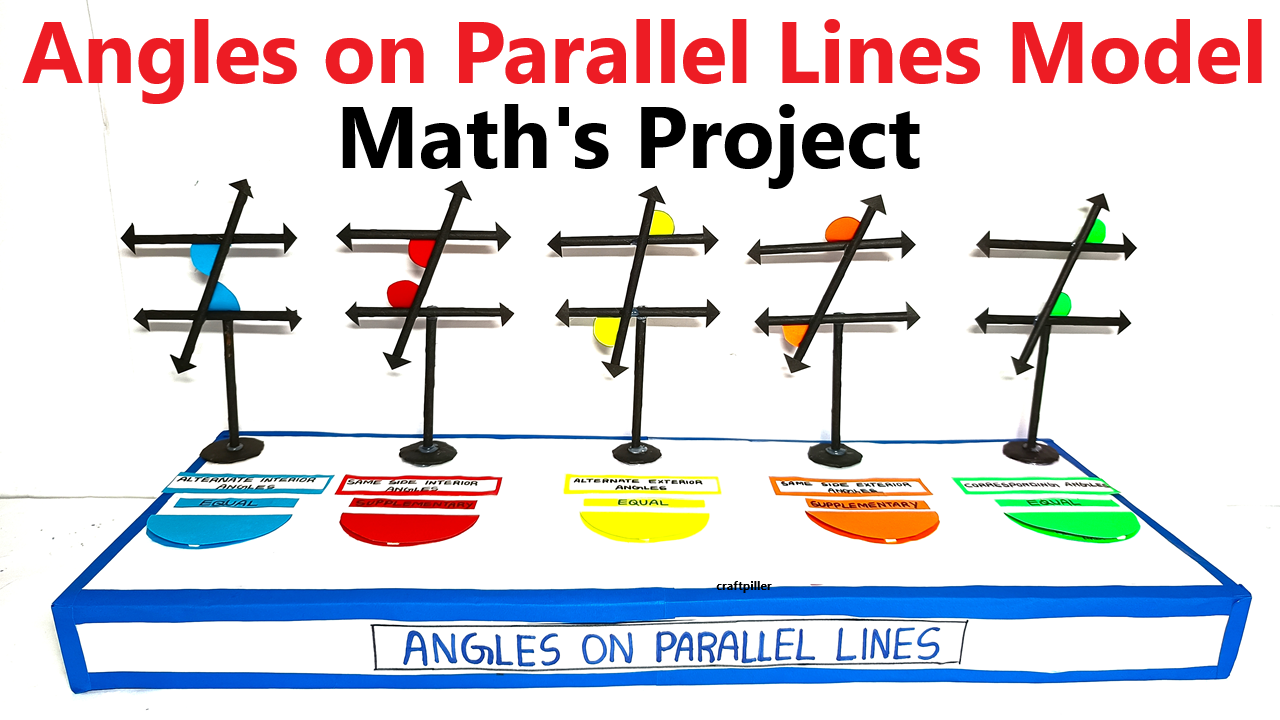
How to make Angles on Parallel Lines Working Model – DIY Math Project

by

Objective:

To demonstrate the different types of angles formed when a transversal crosses parallel lines (corresponding, alternate interior, alternate exterior, and consecutive interior angles) using simple materials like color paper, straws, and cardboard.

Materials Required:

  1. Cardboard (to create the base of the model)
  2. Color paper (for labels and angle markings)
  3. Straws (to represent the parallel lines and transversal)
  4. Scissors
  5. Glue or tape (to fix the straws and paper)
  6. Ruler (for precise measurements)
  7. Markers or pens (to label angles)
  8. Protractor (to measure and confirm angles, optional for reference)

Steps to Build the Model Angles on Parallel Lines:

  1. Prepare the Base:
    • Cut a piece of cardboard large enough to serve as the base for the model.
    • Use color paper to cover the cardboard or leave it plain for a simple look.
  2. Create Parallel Lines:
    • Take two straws and place them parallel to each other on the cardboard.
    • Secure them with glue or tape to the base, ensuring they remain parallel.
  3. Add the Transversal:
    • Take another straw and position it across both parallel straws at an angle.
    • Secure the transversal straw with glue, making sure it intersects both parallel lines.
  4. Label the Angles:
    • Use markers or colored paper to label the different angles formed by the transversal crossing the parallel lines:
      • Corresponding Angles: Angles that occupy the same relative position at each intersection (e.g., top left angle at one intersection corresponds to the top left angle at the other intersection).
      • Alternate Interior Angles: Angles that are on opposite sides of the transversal but between the parallel lines (e.g., the angle above the transversal at one intersection corresponds to the angle below it on the opposite side).
      • Alternate Exterior Angles: Angles that are on opposite sides of the transversal and outside the parallel lines (e.g., the angle outside the parallel lines, on the left of the transversal, corresponds to the angle on the right).
      • Consecutive Interior Angles: Angles that are on the same side of the transversal and between the parallel lines (e.g., the angle above the transversal on the left corresponds to the angle below it on the same side).
  5. Color Paper Markings:
    • Cut small pieces of colored paper to highlight different angles, using each color for one type of angle. For example, use blue for corresponding angles, red for alternate interior angles, and so on.
    • Label each angle accordingly with the name and a brief description.
  6. Optional – Confirm Angles with a Protractor:
    • Use a protractor to measure the angles formed and ensure they are accurate, demonstrating the concept of parallel lines and transversals.

Detailed Description of Each Angle Type:

  1. Corresponding Angles:
    • Definition: These angles are on the same side of the transversal and in corresponding positions at each intersection.
    • Example: Angle 1 and Angle 2 are corresponding if they occupy the same relative position in both intersections (top left angle of both intersections).
    • Property: Corresponding angles are equal in measure.
  2. Alternate Interior Angles:
    • Definition: These angles lie on opposite sides of the transversal and inside the parallel lines.
    • Example: Angle 3 and Angle 4 are alternate interior angles because they lie between the two parallel lines but on opposite sides of the transversal.
    • Property: Alternate interior angles are equal in measure.
  3. Alternate Exterior Angles:
    • Definition: These angles are on opposite sides of the transversal and outside the parallel lines.
    • Example: Angle 5 and Angle 6 are alternate exterior angles as they are outside the parallel lines but opposite each other.
    • Property: Alternate exterior angles are equal in measure.
  4. Consecutive Interior Angles (Co-interior Angles):
    • Definition: These angles lie on the same side of the transversal and between the parallel lines.
    • Example: Angle 7 and Angle 8 are consecutive interior angles because they are on the same side of the transversal, between the two parallel lines.
    • Property: Consecutive interior angles are supplementary (they add up to 180°).

How It Works:

  1. Interactive Learning:
    • As students view the model, they can identify and match each type of angle.
    • Use the colored paper markings to reinforce the angle types and help visualize their relationships.
  2. Angle Relationships:
    • Discuss the equalities of corresponding, alternate interior, and alternate exterior angles.
    • Explain the supplementary nature of consecutive interior angles, helping to reinforce geometry concepts.

https://www.youtube.com/@howtofunda

Leave a Comment