In this video blog post we write about making of the corresponding angles model working model for BEd and Teachers
Creating a corresponding angles model using cardboard and colored paper is a great way to visually understand the concept of corresponding angles in geometry.
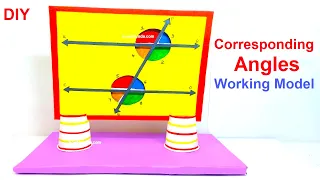
Here’s a step-by-step guide to making a simple corresponding angles model:
Materials you’ll need:
- Cardboard (thick and rigid)
- Colored paper (two or more different colors)
- Paper Cups for Stand
- Scissors
- Ruler
- Pencil
- Glue or adhesive tape
- Markers or colored pens (optional, for additional details)
Step-by-step process:
- Cut out the base:
- On the cardboard, draw and cut out a large square or rectangle to serve as the base of your model.
- Create angle strips:
- Take one colored paper and cut out several long, thin strips. These strips will represent the sides of the angles in your model. The width of the strips should be uniform.
- Label the angle strips:
- Using a pencil or marker, label each strip with an angle measurement (e.g., 30°, 45°, 60°, etc.). Make sure to have at least two strips of each angle measurement.
- Attach the angle strips:
- Take the angle strips and attach them to the base (cardboard) in a way that they form pairs of corresponding angles. For example, if you have a strip labeled 30°, find another strip labeled 30° and place it diagonally across from the first one so that the two strips form an “X” shape. Repeat this for all angle measurements.
- Glue or tape the angle strips:
- Use glue or adhesive tape to secure the angle strips onto the base. Make sure they are firmly attached.
- Once your corresponding angles model is complete, you can use it to visually understand the concept of corresponding angles. Experiment with different angle measurements and observe how the corresponding angles are congruent (equal) to each other.
This model will help you see how corresponding angles are formed when a transversal (a line that intersects two or more other lines) cuts through two parallel lines. Corresponding angles are located on the same side of the transversal and in the same position relative to the two parallel lines.
#correspondingangles #workingmodel #tlm #craftpiller #mathsmodel #maths #model #diy

