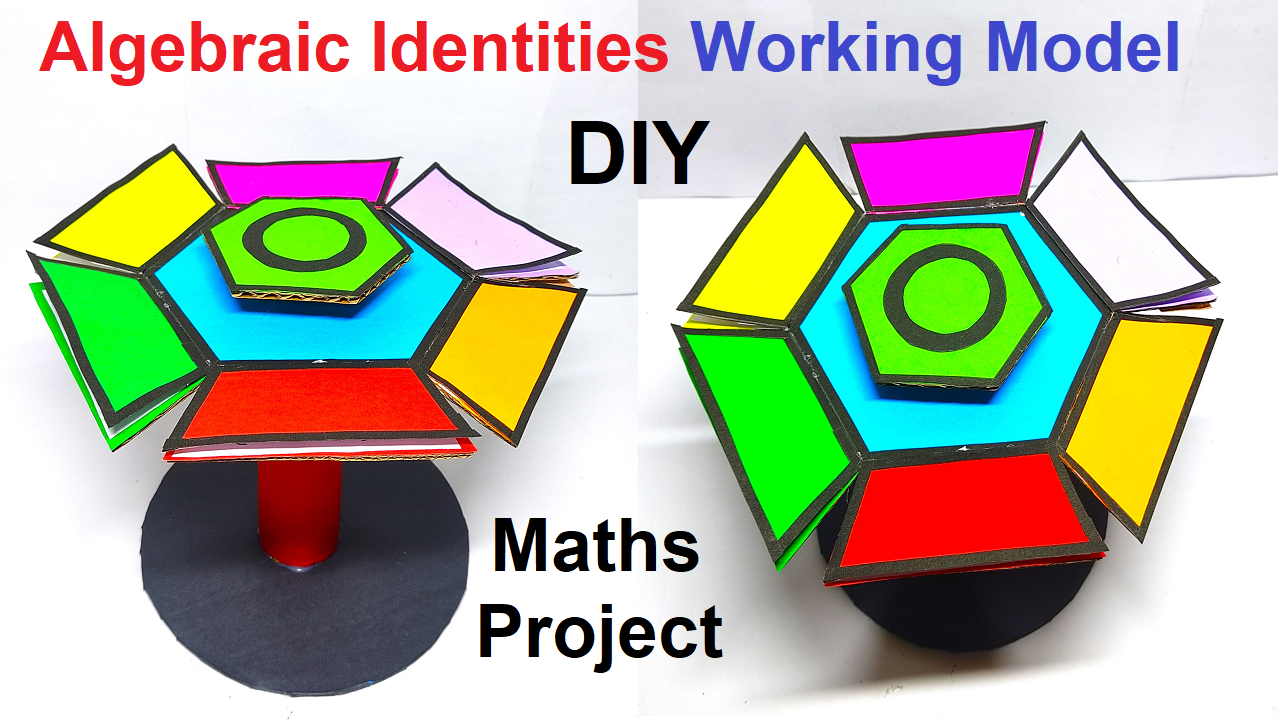
Creating a working model for algebraic identities using cardboard is a great way to visually represent and understand mathematical concepts.
One common algebraic identity is the “Square of a Binomial.” Let’s create a model to represent the identity (�+�)2(a+b)2.
Materials Needed:
- Cardboard
- Colored paper or markers
- Ruler
- Scissors
- Pencil
- Glue
Model Construction:
1. Create the Base:
- Cut a square piece of cardboard to serve as the base of your model.
2. Draw the Square:
- Use a ruler and a pencil to draw a large square on the cardboard. This square represents (�+�)2(a+b)2.
3. Divide the Square:
- Divide the large square into four equal smaller squares. Each side of the smaller squares should be labeled as �a, �b, �a, and �b.
4. Cut Flaps:
- From one side of each smaller square (except the bottom one), cut flaps along the sides labeled �a and �b, leaving the bottom square intact.
5. Fold and Label:
- Fold the flaps along the cut lines to create triangular flaps. Label each flap with the corresponding term (�a, �b, or ��ab).
6. Coloring (Optional):
- Use colored paper or markers to distinguish between �a and �b squares. You can color the flaps differently to represent the terms.
7. Assembly:
- Fold and glue the flaps into place, forming the original large square with the terms �2a2, �2b2, and 2��2ab.
By creating a physical representation of algebraic identities, students can gain a deeper understanding of mathematical concepts. This hands-on approach helps make abstract ideas more concrete and accessible.